Кривизна пространстваУчебные материалы по биологии / Устройство Вселенной / Кривизна пространства
. Геометрия на плоскости - эвклидова (неискривленная) геометрия. Можно указать признак: сумма углов в треугольнике равна 180 .
. Геометрия Римана (искривленная), треугольник на шаре, сумма углов в треугольнике больше 180 .
. Геометрия Лобачевского (искривленная), треугольник на седловине, сумма углов в треугольнике меньше 180 .
Геометрии Римана и Лобачевского имели огромное значение для развития теории относительности. В частности, математик Герман Минковский применил неэвклидовы геометрии для объяснения теории относительности. Эйнштейн предположил в общей теории относительности, что кривизну пространства можно объяснить наличием гравитационного поля, или поля тяготения. Он предложил использовать неинерциальные системы отсчета в качестве инерциальных, в которых имеется поле тяготения.
Таким образом, гравитационное поле, по предположению Эйнштейна, является причиной искривления пространства.
От чего будет зависеть гравитационное поле и кривизна пространства? На этот вопрос можно ответить, рассматривая закон всемирного тяготения.
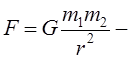сила гравитационного притяжения.
Поскольку масса (m) зависит от плотности вещества и объема тела (
, где - плотность вещества; V - объем тела), то в конечном счете сила гравитационного притяжения зависит от плотностей веществ взаимодействующих тел. Кроме того, сила гравитационного притяжения (величина гравитационного поля) зависит от расстояния (r) между телами, и следовательно будет изменяться при движении тел. Поэтому мы можем сказать, что гравитационное поле и кривизна пространства зависят от плотности вещества и его движения.
В пределах нашей солнечной системы и даже за ее пределами пространство может считаться эвклидовым. Однако во Вселенной существуют объекты, вблизи которых пространство является существенно искривленным. К таким объектам относятся массивные тела, например Солнце, звезды, черные дыры и др.
Оказалось, что и развитие таких объектов, как сама Вселенная, зависит от плотности материи в ней.
Смотрите также
Макрофитон и фитопланктон озера Белое
Введение
В
водных экосистемах растения выполняют ряд жизненно важных, тесно связанных
между собой экологических средообразующих и средозащитных функций:
фильтрационную, окислительную ...
Ткани и их функции в растительных организмах
Предисловие
Структурная и функциональная целостность высших растений
достигается благодаря многочисленным многоуровневым приспособлениям, среди
которых дифференциация единого тела на ...
Религия и наука о происхождении человека на Земле
Введение
Тема
«Религия и наука о происхождении человека на Земле» на протяжении множества
веков вызывает достаточно споров и является актуальной и в наши дни. Изначально
мной была вы ...